Tags: probability
<< previousnext >>I played a lot of basketball during lockdown. I had free time, there was a basketball hoop outside my house, and I had recently watched The Last Dance, the hit basketball documentary about Michael Jordan and the Chicago Bulls. The time was ripe for my basketball ascendance.
Yet my father still managed to beat me at Around the World. Around the World is a basketball game where your objective is to score from each of several positions around the hoop. And my father beat me at it, despite all my practice, and despite the fact that he had never played much basketball in his life.
This made me wonder -- how much better than someone do you need to be in order to beat them consistently at Around the World? That's the question we're going to answer in this article, using tools from probability. By the end, we'll have produced some cool graphs (if you're into that sort of thing), and we'll have definitively answered the question of whether your granny can beat Michael Jordan at basketball.

Around the World is a race. Players take turns shooting from set positions around the hoop. A player's turn ends when they miss a shot. The winner is the first player to score a shot from all positions. In my variant, we had to score 7 shots, spaced at regular intervals in a semi-circle around the hoop (see above).
Another way to look at it is that the winner is the person who misses the fewest shots before scoring 7 times. And this can be modelled using what is known as a Pascal distribution. Given that a player scores each shot with probability , the probability that they miss shots before finishing the game is
Where did this ugly-looking expression come from? Well, there are sequences of shots (binomial coefficient formula) where the player misses shots before finishing. Why that many!? The player takes shots in total. The last shot has to be a success, as that's when the player finishes the game. This leaves shots, of which we choose to be successes. As for , it's the probability of a single sequence of shots where the player misses shots before scoring 7.
Now that we've hand-wavingly derived the probability formula, what does the distribution look like for different values of ? How many shots should you expect to miss at different skill levels?
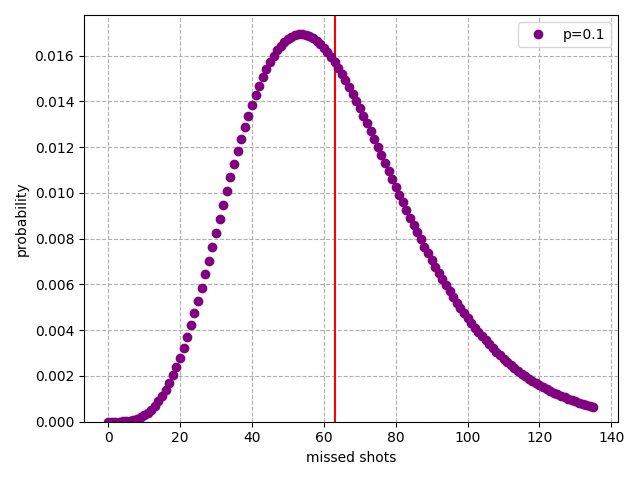
Here's the distribution when . This is roughly granny-level shooting ability. A granny musters enough energy to hurl the ball in the general direction of the hoop, and it happens to go in, about 1 in 10 times. On average, it takes more than 60 misses before granny finishes the game (indicated by the red line).
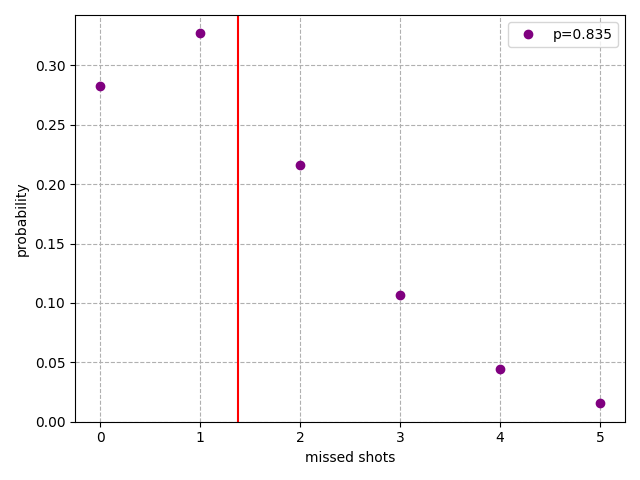
Michael Jordan's average free throw percentage over his career was 83.5% (ref), so let's look at . We see that it would be common (3/10 games) for MJ to not miss a single shot, and the other player wouldn't even touch the ball if MJ was the starting player. On average, we'd expect MJ to miss slightly more than 1 shot.
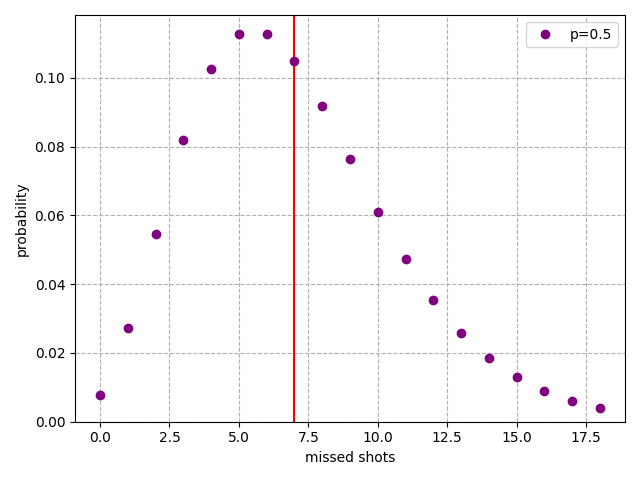
Finally, between the two extremes, here's . This player misses an average of 7 shots before finishing. It's like me on a good day.
Our goal is to estimate the win probability of one player versus another. Me versus my dad. Michael Jordan versus your granny. Michael Jordan versus Michael Jordan. And so on. To do that, we'll have to define some new variables. Let be the event of a win for the first player, let be the number of shots they miss, and let be the same but for the second player. Also let and be the shot success probabilities of each player. We can now state the probability of the first player winning:
We know the value of from above, except that is swapped for . And we get by summing up for all :
Why and not ? This is because the first player wins if they miss the same amount of shots as the second player, as the game ends before the second player can finish their shots.
With that out of the way, here's a heat map of the first player's win probability, for varying values of and 1. It ranges from black (the first player will almost certainly lose) to white (the first player will almost certainly win). When we compare Michael Jordan as the first player () to a granny as the second player (), the result is blindingly white. Granny doesn't stand a chance.
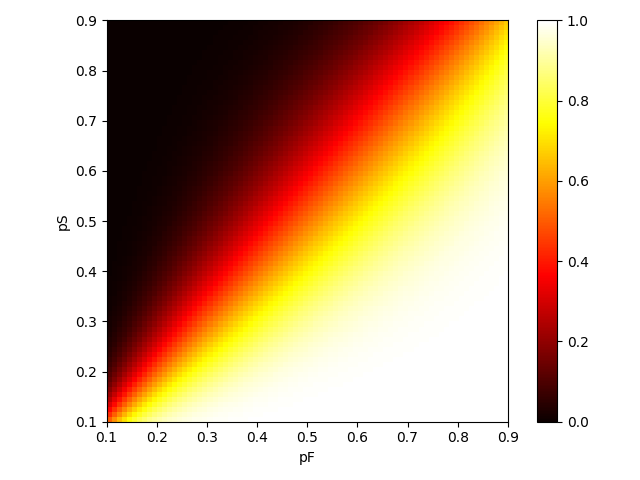
Another observation: the pixel in the bottom left corner is a reddy orange, which is close to a 50% win rate for the first player. The pixel in the top right corner is an orangey yellow, around 70%. It seems that going first gives a bigger advantage to more skillful players.
Here's similar data in table format, with results rounded to 4 decimal places. increases as you go down the table, while increases as you go left to right.
| pF/pS | 0.1 | 0.25 | 0.4 | 0.5 | 0.6 | 0.835 |
|---|---|---|---|---|---|---|
| 0.1 | 0.5059 | 0.0374 | 0.0032 | 0.0007 | 0.0002 | 0.0 |
| 0.25 | 0.9665 | 0.5162 | 0.162 | 0.0654 | 0.0245 | 0.0016 |
| 0.4 | 0.9974 | 0.8637 | 0.5291 | 0.3208 | 0.1726 | 0.0234 |
| 0.5 | 0.9994 | 0.9499 | 0.7382 | 0.54 | 0.3514 | 0.0738 |
| 0.6 | 0.9998 | 0.9833 | 0.8742 | 0.7311 | 0.554 | 0.1736 |
| 0.835 | 0.9999 | 0.9993 | 0.9894 | 0.965 | 0.9124 | 0.6235 |
This confirms our observation that going first gives a bigger advantage to stronger players. When a granny plays a granny, the first granny has only a small advantage -- a 50.59% chance of winning. Whereas a Michael Jordan who plays first has a 62.35% chance of beating a second Michael Jordan. The game tends to end in fewer turns at higher levels of play, which makes the extra turn at the start count for more.
Let's say that my father, a mediocre player, has a score rate of 40%. And that I, a slightly less mediocre player, have a score rate of 50%. Then my father would still be expected to beat me in about 3/10 games. I guess this explains my humiliating defeats.
As for the scenario we posed at the beginning of the article: it's almost impossible for a granny to beat Michael Jordan. But there's a chance.
See the code here.
As you might have guessed, we don't compute the entire infinite sum to generate this graph. We stop after enough terms have been added that the error in the result is small. ↩
I'd be happy to hear from you at galligankevinp@gmail.com.