Tags: simulation
next >>Boarding a plane, you wait behind a man so unwashed that you can almost see a stink cloud emanating from his trenchcoat. Two rows ahead, an old woman struggles to lift her humongous suitcases, each of which is large enough to fit her inside. Behind you is a red-eyed, defeated mother, holding a shrill baby. "There has to be a faster way to get through this," you think to yourself. Then the baby vomits into your backpack.
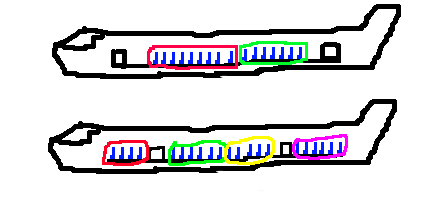
Consider a typical plane in Europe, such as Ryanair's Boeing 737-800. 2 entrances for passengers, one at each end of the plane. 200 seats spread across 32 rows, with an aisle down the middle.
Passengers board using the entrance that is closest to their seat. This makes boarding more efficient because passengers from the back and passengers from the front don't have to climb over each other.
Here's an idea: what if we moved the entrances to 1/4 and 3/4 of the way through the plane, respectively, rather than placing them at the ends. Pre-boarding, passengers would still be sorted into 2 groups based on how close their seats were to the entrances. During boarding, however, they would effectively be split into 4 groups: those who turned left at the 1st entrance, those who turned right at the 1st entrance, those who turned left at the 2nd entrance, and those who turned right at the 2nd entrance.

This would further reduce the interference between passengers, and, in theory, further reduce boarding times. We're going to run an extremely simple simulation in Python to test this theory.
The simulation, made using the pygame library, runs in a series of "time steps". It takes 1 time step for a passenger to move between rows, and 5 time steps for a passenger to put their luggage into the rack and take their seat. These numbers were chosen arbitrarily.
We first run a simulation with entrances at the ends of the plane. Then we run a version with centered entrances.
In this case, the entrances-at-ends design takes 239 time steps before everyone is seated, while the centered-entrances design takes 209 time steps, which is 12% less.
Just to be scientific about it, we can run both versions of the simulation 10,000 times and see what the average number of time steps is for each. Here are the results:
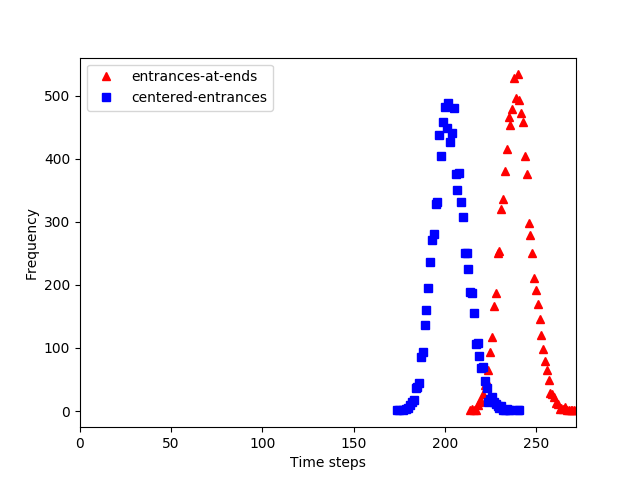
The centered-entrances design is, on average, ~15% faster in this run of the simulation.
Of course, there may be engineering or safety issues that prevent plane manufacturers from playing around with their plane designs like this. Perhaps placing the entrances at the ends gives space for more seats. Perhaps the wings and emergency exits get in the way of centered entrances. Etcetera.
Whatever the case, it's a nice distraction to think about as the trenchcoat stink cloud wafts its way towards you and the baby in your vicinity makes threatening heaving motions.
Further thoughts on the efficiency of plane boarding can be enjoyed in this fun video by CPG Gray, which doesn't mention plane design but discusses a number of algorithms for faster boarding.
For the curious, here's the script used to run the simulation and animate it.
I'd be happy to hear from you at galligankevinp@gmail.com.