Random RGB values that average to N; or, Pointlessness and Probability

In other words, we have to generate a random RGB value so that (R+G+B)/3=A, or equivalently, R+G+B=3A. We'll solve this problem using the Python programming language and learn some neat combinatorics along the way.

An attempt

The first algorithm that might come to mind is to generate R, G and B one at a time, ensuring that we satisfy the constrants of the problem at each step. Being RGB, they have to be in the range 0-255. We must also ensure that it remains possible to satisfy R+G+B=3A. If we stay within these constraints, then we will always end up with a valid RGB value with an average of A, no matter what value A has. Note that there's always at least one solution to R+G+B=3A, and that's the RGB value (A,A,A).

import random as rd
def generate_rgb(A):
    S = 3*A
    # Generate a random value for R, ensuring that:
    #  1) 0 <= R <= 255
    #  2) R <= 3A
    #  3) R >= 3A - 2*255
    # We need #3 because otherwise, even with G=B=255, we'd
    # have R+G+B<3A and the average of R, G, B would be less than A.
    R = rd.randint(max(S - 2*255, 0), min(S, 255))
    S -= R
    # Similar conditions to satisfy for G.
    G = rd.randint(max(S - 255, 0), min(S, 255))
    S -= G
    B = S
    return R, G, B

This approach seems reasonable, and if we run a test that checks whether the resulting RGB values have an average of A (for A=1), it passes with flying colours.

A = 1
rgbs = [generate_rgb(A) for _ in range(100000)]
print("PASS" if all(sum(rgb) == 3*A for rgb in rgbs) else "FAIL")
# output: PASS

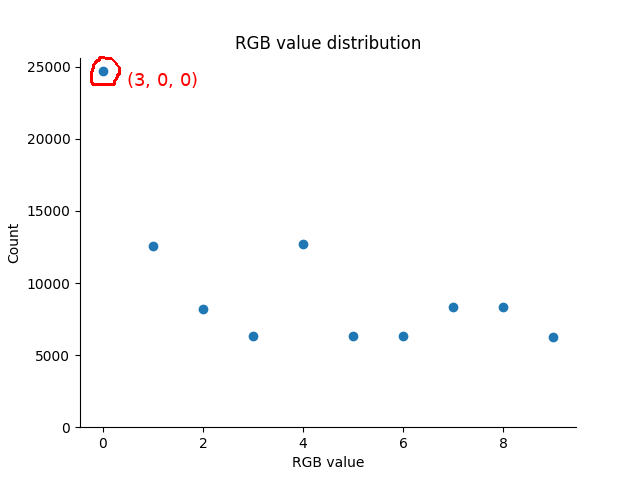
However, this doesn't give us the full picture. Besides ensuring that R+G+B=3A, we also need to check that all of the possible RGB values are equally likely to appear, since the problem statement requires randomness. Graphing the frequency of the possible values, we see that this is not the case.

(3,0,0) is the most likely value by far at ~25%. The pie chart below illustrates why this is the case.

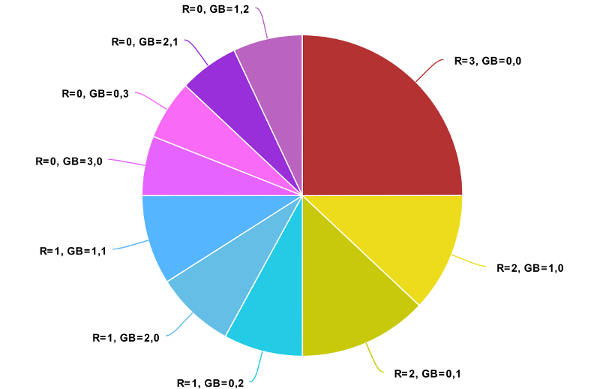
Our algorithm picks an R value from 0, 1, 2 and 3 with equal probability, so 25% of the probability pie is assigned to each possible R value. The quarter slices of pie are then further divided by the number of possible GBs that satisfy R+G+B=3A. For R=3, the only valid GB value is (0,0), and so the RGB value (3,0,0) ends up with a whole 25% slice of probability. For R=1, the possible GBs are (0,2), (2,0) and (1,1), so the 25% slice is divided between the RGB values of (1,0,2), (1,2,0) and (1,1,1), giving them each a probability of ~8.3%.

Well, I'll be damned! What's the darn-tootin' solution, then?

The issue with the first algorithm is our false assumption that all possible R values are equally likely. In the case of A=1, P(R=3) -- the probability that R is 3 -- is 0.1, since 1/10 of the possible RGB values have R=3. Meanwhile, P(R=1)=0.3, since 3/10 of the possible RGB values have R=1.

Hence, before picking R at random, we have to calculate the probability of each of its possible values.

(Syntax note: #{blah} here means "the number of blah", so #{GB values that sum to 3A-r} is the same as saying "the number of GB values that sum to 3A-r").

You can see why this gives P(R=3)=0.1 and P(R=1)=0.3, given that #{GB values that sum to 2}=3, #{GB values that sum to 0}=1, and #{RGB values that average to 1}=10.

How do we calculate this for any 'r' and any 'A'? Let's consider the numerator and the denominator separately.

P(R=r): the numerator

G and B can be any value in the interval

[\text{max}(3A-r-255, 0), \text{min}(3A-r, 255)]

, so all we're doing is calculating the length of this interval. It's similar to what we did in the first algorithm.

To convince yourself that it's correct, consider the case where A=87, 3A=261 and r=1. We have 3A-r=260. The GB values that sum to 260 are (255,5), (254,6), ..., (5,255). There are 255-5+1=251 such values. This agrees with the expression above. Repeat for various values of A and r.

P(R=r): the denominator

The expression for #{RGB values that average to A} is below. It looks scary, but we'll explain each part in an intuitive manner.

{3A+3-1 \choose 2} \color{blue}{-3{3A+3-1-256 \choose 2}} \color{red}{+3{3A+3-1-2\cdot 256 \choose 2}}

(Syntax note: () is the "binomial coefficient" function, which can also be written as nCk: "the number of combinations of k things that you can choose from n things". For example, 10C2 is the number of possible pairs of socks you could make from 10 socks).

The first part, in black, gives the number of ways that R, G and B can add up to 3A. Using the nCk syntax, we can write it as {3A+3-1}C{2}, or "the number of ways to choose 2 things from 3A+3-1 things".

But why is "the number of ways that R, G and B can add up to 3A" the same as "the number of ways to choose 2 things from 3A+3-1 things"?

Let's consider an example where A=2, 3A=6. Imagine that we have the numbers 1-6 lined up with spaces between them. We have to put "partitions" in 2 of the spaces in order to divide 3A=6 between R, G and B, as seen below.

Here, R=2, G=3 and B=1. We have 3A-1=5 spaces, and we have to insert partitions into 2 of them, which gives {3A-1}C{2} possible combinations.

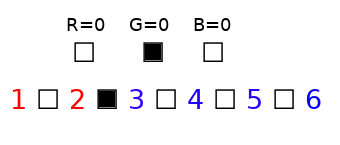
HOWEVER, to complete the first part we also have to account for the case where any of R, G or B are 0. For that reason, we need 3 extra spaces acting as flags that let us set each of R, G and B to 0. If we put a partition in one of these spaces, it means that the corresponding R/G/B is set to 0.

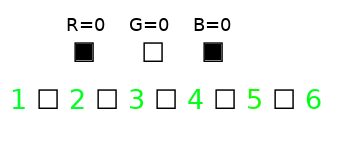
To conclude: including the zero flags, we need 3A-1+3 spaces, of which we pick 2. And like that, we can make sense of the first part of the expression, {3A-1+3}C{2}.

We need the second part of the expression because, in the first part, we unwittingly allowed R>255, G>255 and B>255. The intuition is the same as the first part, except we remove 256 numbers and assign them to one of R, G or B. The remaining 3A-1+3-256 spaces are divided among R, G and B like before, by inserting partitions into 2 spaces, and there are {3A-1+3-256}C{2} ways to do so. And we multiply by 3 for the 3 cases: R>255, G>255 and B>255.

Here's an example where 3A=264. We set aside 256 numbers for R, then partition the remaining ones like we did before. If we "enabled" the R=0 flag, then the final value of R would just be 256.

The final part of the expression for #{RGB values that average to A} is needed because, in the second part, we double-subtracted the case where more than one of R, G and B are greater than 255, so we have to re-add them. First we subtracted combinations where R>255, which includes combinations where G>255. Then we subtracted combinations where G>255, which includes combinations where R>255. In the end, we've double-subtracted the combinations where R>255 as well as G>255.

In this example, A=173 and 3A=519. We set aside 256 numbers for R and 256 numbers for G, then partition the remaining 7 numbers between R, G & B like before.

There are 3A+3-1-2*256 spaces, of which we pick 2. There are {3A+3-1-2*256}C{2} ways to do this. Multiply by 3 because there are 3 different pairs of R, G & B that can both be >255, and out pops the final part.

And with that, we understand how to calculate #{RGB values that average to A}. Which, in turn, allows us to calculate P(R=r)!

Putting it all together: using P(R=r) to generate random RGB values

The hardest part is done. Now we pick R randomly based on P(R=r). After that, G and B can be determined from a random choice with uniform probability like in the "first attempt" algorithm.

import random as rd
from scipy.special import comb

def generate_rgbs(A, n=1):
    S = 3*A
    num_rgbs = num_rgbs_that_sum_to(S)
    # R can't be smaller than 3A - 2*255. Otherwise, even with G=B=255, we will have:
    #   R + G + B = (3A - 2*255 - blah) + 255 + 255 = 3A - blah < 3A.
    # Similarly, R can't be bigger than 3A.
    # We also need to ensure that R is in the range [0, 255].
    R_possible_values = list(range(max(S - 2 * 255, 0), min(S, 255) + 1))
    R_probabilities = [num_gbs_that_sum_to(S - r) / num_rgbs for r in R_possible_values]
    return [generate_rgb(S, R_possible_values, R_probabilities)
            for _ in range(n)]

def num_rgbs_that_sum_to(S):
    """Outputs number of RGB tuples that sum to 'S'."""
    K = 3 # R, G, B
    return (comb(S + K - 1, K - 1)
        # Remove cases where R, G or B are >255, since
        # these are not allowed.
        - 3 * comb(S + K - 1 - 256, K - 1)
        # Re-add the case where >1 of R, G and B are >255, since
        # they were subtracted twice in the previous bit.
        + 3 * comb(S + K - 1 - 2 * 256, K - 1))

def num_gbs_that_sum_to(S):
    return min(S, 255) - max(S - 255, 0) + 1

def generate_rgb(S, R_possible_values, R_probabilities):
    """Generates R,G,B that sum to S given pre-computed probabilities
    for possible R values."""
    # Weighted random choice based on P(R=r).
    R, = rd.choices(population=R_possible_values, weights=R_probabilities)
    S -= R
    G = rd.randint(max(S - 255, 0), min(S, 255))
    S -= G
    B = S
    return (R, G, B)

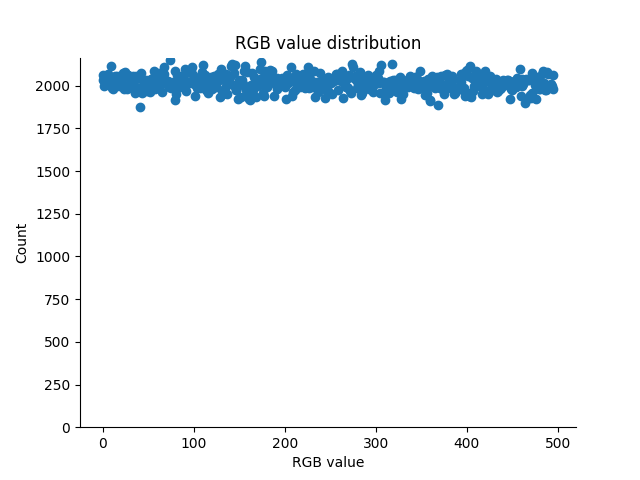
Besides generating valid RGB values, all of the possible RGB values seem to have an equal probability of being generated (here, for A=245).

Conclusion

We've battled through the combinatorics and come out the other side with a working algorithm. An extension to the algorithm that might be interesting would be to make it work for the "general" case. That is, generate a random tuple V = (V1, V2, ..., Vn) such that the average (V1+...+Vn)/n is A, and where Bl <= Vi, A <= Bu. The combinatorics behind this would be similar to what we did above.

A different approach to the problem would be to generate random RGB values directly from the sequence of valid values rather than going through the rigmarole of calculating probability distributions. In other words, if there are N possible RGB values, we generate a random number 'k' between 1 and N and pass it to our magic function 'f' so that f(k) outputs the kth RGB value with the target average.

That's all for now. Tune in for the next episode of Problems That Don't Need to Be Solved, where we'll be looking at Rubix Cubes.