
In the image below is a triangulation pillar, or triangulation station. Thousands of years ago, aliens placed this pillar at the top of Benbulbin mountain in Ireland. It contains advanced technology that allows the aliens to monitor human civilisation from across the galaxy.

Just kidding. It's a block of concrete that was placed there by humans in the past 200 years, and was used to create maps of Ireland in the time before satellites. In this article we'll see how those maps were constructed (using the law of sines from trigonometry!), and we'll also see how measurement error could affect the mapping.
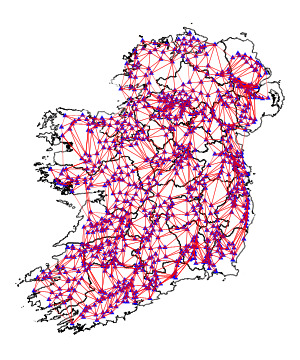
To understand the idea behind triangulation pillars, let's see how they're distributed throughout Ireland. Here's a map of that distribution. The red triangle corresponds to the Benbulbin pillar shown above. I got the pillar coordinates from here, and the county boundary coordinates from here.
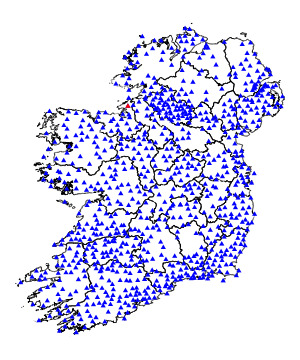
The first step in creating a map is to form a triangle mesh between all the pillars. Since I don't know how the pillars were connected in the past, I used Python's scipy.spatial.Delaunay to do so. Each pillar is part of at least one triangle in the mesh.
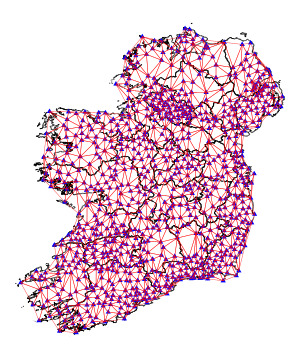
By removing the county boundaries, it becomes clear that the shape of Ireland is captured quite well by the triangle mesh. If we could can figure out the positions of the pillars relative to each other, then we would be able to draw this mesh and it could form the basis of a map of Ireland.
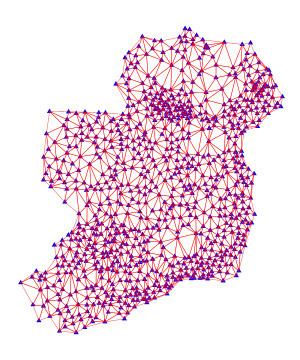
Here's how the mapping works in practice. Once the pillars are in place, the first step in a hypothetical survey is to take a single triangle and measure one of its side lengths. In the Irish Ordnance Survey, beginning around 1827, this base measurement was taken between two pillars along the shores of Lough Foyle in Northern Ireland. The next step in the hypothetical survey is to measure the internal angles of each triangle using a device called a theodolite. Basically, you stand at one of the pillars, which for visibility should be built in a high place, and put light sources at two of its neighbouring pillars. The theodolite can accurately determine the angle between the neighbouring lights, thus enabling you to determine the angle at that corner of the triangle.
Based on these measurements -- a single side length and the angles of all the triangles -- a full map of the country can be reconstructed based on the law of sines. Given the internal angles of a triangle and a single side length, the law of sines yields the two remaining side lengths.
This is easiest to explain through an example. Suppose we're standing at Benbulbin, which is neighboured by triangulation pillars at Mullaghmore and Truskmore. Let's say we want to calculate the distance to Truskmore, labelled x in the diagram below. We've already used our theodolite to measure the angles between the pillars, and we measured the straight-line distance from Benbulbin to Mullaghmore (here, 10km) using a really really long stick.
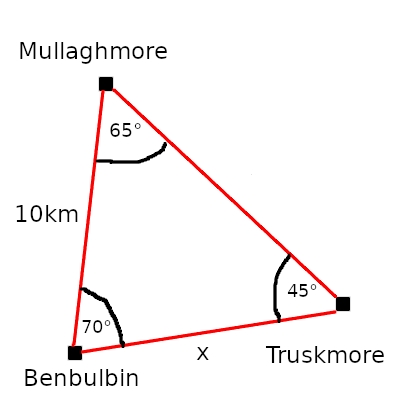
According to the law of sines, you can take the sine of any angle of a triangle and divide by the length of the opposite side, and it gives you the same result. Thus,
Solving for x gives a distance of about 9.72km. Using this new distance estimate, we could then estimate the distance from Benbulbin and Mullaghmore to other pillars, and so on and so forth, until we know the relative positions of all the pillars in Ireland.
What happens if we mess up the initial distance measurement? I'm glad you asked, because that's what we're going to examine next.
Let's say we've accurately measured the angles between all the pillars on the map above. We don't know how far apart they are, though. So our next step is to measure the distance between a single pair of pillars. Let's say we measure the distance between Scalp Mountain and Creehennan Hill, both along the shores of Lough Foyle. Assuming the measurement has 0% error, that distance can be propagated through the whole triangle mesh using the law of sines, and the map of triangulation pillars can be reconstructed exactly. I'm not even going to bother showing the results of this process, because it would be an exact copy of the map from before.
However, let's say the initial measurement is 25% shorter than it should be. The result is a shrunken triangle mesh that evidently does not capture the area of Ireland:
Honestly, it's more robust than I expected. I thought it would explode in different directions. Perhaps the error cancels out as pillars get pulled in different directions. We do see that the individual triangles overlap, however, and so our hypothetical cartographer would at least be aware that they had made a serious error in their initial measurement.
I took that picture at Benbulbin, so I can appreciate how hard it must have been to capture so many measurements back in the day. There are 868 pillars in the dataset I looked at, and I wince at the thought of climbing Benbulbin 868 times.
ANYWAY, follow-up links:
I'd be happy to hear from you at galligankevinp@gmail.com.