The bit-twiddling magic of two's complement, explained

2021-12-14

The motivation for two's complement, how it works, and where the bit-twiddling comes from.

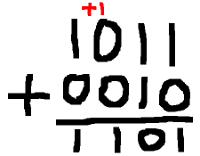
Tags: programming

If you've ever taken a computer science class, then you've probably heard of two's complement. What you might have been told is that it's a system for representing positive and negative numbers in computers, and that to convert a number to two's complement form, you invert all the bits and add 1.

"Okay," you may have thought to yourself on hearing this information, unconvinced, "but doesn't flipping the bits and adding 1 seem kinda arbitrary? And what's the POINT of two's complement?"

These are the questions I will attempt to briefly answer.

Here's an example to reacquaint ourselves with two's complement. Let's say you have a decimal number, $5_d$. The little 'd' stands for decimal. Assuming you have 4 bits, $5_d$ is $0101_b$ in binary (where the little 'b' stands for binary). To convert this number to two's complement, you change the 0s to 1s and the 1s to 0s, giving $1010_b$, and then you add 1, giving $1011_b$. The number $1011_b=11_d$ is treated as $-5_d$ in the two's complement system.

The POINT of two's complement, or at least one of the points, is that it allows you to take the same circuitry with which you add, multiply and subtract positive numbers, and use it to add, multiply and subtract negative numbers. This means you don't need complicated circuitry just for negative numbers.

Let's explore why negative numbers might require complicated circuitry. Remember how they taught you to add numbers digit-by-digit in school? Computers add numbers in pretty much the same way. They go through the digits from least significant (rightmost) to most significant (leftmost) and add them up individually. If the sum of two digits is too big to store in a single digit, then you have to carry a 1 over to the next digit, as shown in the example below.

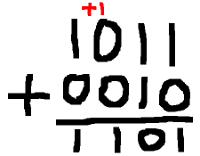
This algorithm is easy to model with logic gates because the addition of two digits depends only on the addition of the previous two digits (and whether there was a carry). It doesn't have to look 10 digits ahead, or 10 digits behind. Just 1 behind. For this reason, the gates can be chained together sequentially, making the circuit straightforward and efficient.

The subtraction algorithm you learned, on the other hand, is a pain in the ass. If you'll recall, it proceeds from right to left, like addition does. But if the negative digit is larger than the positive digit, you have to look arbitrarily far ahead in order to "borrow" from a more significant positive digit.

This means that the logic gates that perform subtraction for the rightmost bit have to be connected to the leftmost bit somehow -- and all the other bits, too! The resulting circuit will be a tangled mess, like a big ball of hair. Also, if you have an explicit flag that says whether a number is positive or negative, then you need logic to handle updates to this flag, too.

But what if... WHAT IF, my friend, you could use the straightforward addition algorithm, but for negative numbers? And what if I told you, my dear friend, that two's complement allows you to do this! (Please be my friend). It allows you to treat negative numbers as if they were regular, boring old positive numbers, and avoid the ball of hair.

How exactly does two's complement work? Forget about the bit-twiddling for now. Let's say you have 8 bits, which can take on $2^8=256$ possible values (indexed from 0 to 255). In the two's complement system, the first half of the numbers in this range, 0 to 127, are their usual positive selves. +0 is mapped to +0, and +127 is mapped to +127.

Here's the tricky part: the next half of the numbers, 128 to 255, are mapped from -128 to -1. This is like saying that the negative counterpart of a number $k \in [0,127]$, i.e. its two's complement, is $t(k)=2^8-k$.

FOR EXAMPLE. The two's complement forms of 0, 1 and 127 (which you can check in the number line above) are:

$$\begin{aligned} t(0)&=2^8-0=2^8\equiv 0 &\pmod{2^8}, \\ t(1)&=2^8-1=255\equiv 255 &\pmod{2^8}, \\ t(127)&=2^8-127=129\equiv 129 &\pmod{2^8}. \end{aligned}$$

A reminder: addition of $b$-bit numbers has to be done modulo $2^b$, because only $2^b$ numbers can be represented. If we add 2 $b$-bit numbers together and they exceed $2^b$, they roll around to 0 and we count from there. So, $256+1$ is $257$, which, modulo (or mod) $2^8=256$, is $1$.

What happens when we add a number and its two's complement form? We get 0, just as if we subtracted the number from itself!

$$\begin{aligned} 0+t(0)&=0+0\equiv 0 &\pmod{2^8}, \\ 1+t(1)&=1+255=256\equiv 0 &\pmod{2^8}, \\ 127+t(127)&=127+128=256\equiv 0 &\pmod{2^8}. \end{aligned}$$

I hope this fact goes some of the way to convincing you that two's complement is a sensible system. That we can take the two's complement of a number, and it will behave like the negative of that number when we add it to something.

Let's say we have $b$ bits, rather than focusing on the 8-bit case specifically. We can now say more generally that, given two numbers $k$ and $l$,

$$k+t(l)=k+2^b-l\equiv k-l \pmod{2^b}.$$

Adding the two's complement form of a number is like subtracting it, under modulo!

Here are some more facts about two's complement.

• If you take the two's complement of a number that's already in two's complement form, you get the number back: $t(t(k)) = 2^b-(2^b-k) = k$. It's the same as negating a negative number, which makes it positive.
• To subtract a number from another number in two's complement, you convert the number you want to subtract into two's complement form, then add it to the other number. (See: the equation above where we add $k$ and $t(l)$). No hairy circuits involved!

Okay. There are two details about two's complement left to discuss. The first detail is the big wart on its backside. The second detail is the bit-twiddling that was used to introduce you to two's complement all those years ago.

The wart on two's complement's bottom is that, as you may have noticed, there's no +128 to match -128 in our 8-bit number line! The two's complement operation applied to 128 gives $t(128)=256-128=128$. That is, the two's complement of 128 is itself. There's no space left to represent both +128 and -128, so we have to map the value 128 to only one of them. I'm not sure why, but the convention is to pick -128. Some things still work as expected: $1+t(128)=128+1=129=t(127)$, i.e. adding 1 to -128 still gives -127. But when we try to negate -128, we get: $t(t(128))=2^b-(2^b-128)=128=t(128)$. -128 can't be negated!

This can be the source of nightmarish bugs. And, since all modern computers use two's complement (if I recall correctly, this fact is going to be enshrined in the C standard), you can't avoid it. If you compile and run the following C code on your computer, it will most probably print -128.

#include <stdio.h>
int main() {
    char n = -128;
    n = -n;
    printf("%d\n", n);
}

And now, here it is. The moment that nobody has been waiting for. Where does the bit-twiddling come from? We have described the two's complement form as $t(k)=2^b-k$, so why is it introduced using bit flips and rogue +1's? I'm not sure why it's introduced in such a confusing way, but the bit-twiddling magic is just a trick to compute $t(k)$ without performing subtraction or needing to store $2^b$ anywhere (which would require $b+1$ bits). This is easiest to demonstrate with an example. Let's say you have 4 bits, and you want to compute the two's complement of $5_d=0101_b$ (using our notation for decimal and binary numbers from before). The two's complement form is

$$\begin{aligned} t(5_d) &= 2_d^4 - 5_d \\ &= 10000_b - 0101_b \\ &= 1111_b + 1_b - 0101_b \\ &= 1010_b + 1_b \\ &= 1011_b. \end{aligned}$$

We split $10000_b$ into $1111_b$ and $1_b$. Subtracting $0101_b$ from $1111_b$ is equivalent to flipping all the bits in $0101_b$ (the same applies for any 4-bit number). Then we add 1. That's where the magic comes from.

• Back to blog
• RSS feed

I'd be happy to hear from you at galligankevinp@gmail.com.