Yet another Wordle solver

2022-02-27

Another one for the pile.

Tags: probability programming data

Like everyone and their dog, I've been playing Wordle. And like everyone and their dog, I've written a Wordle solver. Details below.

But first, a quick introduction to the game. If you haven't come across it yet, Wordle is a language puzzle game. You have 6 guesses to find a secret 5-letter word. Every time you make a guess, you are told which letters are in the correct position, which letters are correct but in the wrong position, and which letters are incorrect.

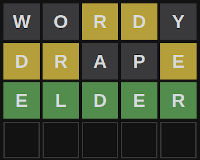
In the example below, our first guess is WORDY. The letters 'R' and 'D' are highlighted in yellow, which means that they're in the secret word somewhere, but not in those positions. The remaining letters ('W', 'O' and 'Y'), are greyed out, which means that they're not in the secret word.

We use that information about the secret word to form our next guess, DRAPE, which tells us that there's an 'E' in the secret word, in addition to the 'R' and 'D'. Finally, we guess ELDER, which turns out to be the correct word. All the letters are highlighted in green, which means they're all in the correct position.

My Wordle solver (let's call it YAWS for short - Yet Another Wordle Solver) is simple. It keeps a list of possible secret words, starting with all 2315 words in Wordle's dictionary. It removes words from the list after each guess, according to the hints it receives. If the solver knows that the secret word begins with 'e', for example, it can remove all words that don't begin with 'e'.

How does YAWS pick the next word to guess? It picks the word that, on average, rules out as many secret words as possible. If we expect there to be an average of 61 possible secret words left after guessing 'raise', then it's a better guess than 'album', which leaves an average of 254 possible secret words, and so YAWS picks 'raise' over 'album'.

Very Slightly More Formally, let's say $S$ is the set of possible secret words, $G$ is the set of allowed guesses (of which there are around 12 thousand), $X$ is the actual secret word (which is random), and $r(g, X, S)$ is the new set of possible secret words after we guess the word $g$. Note that $r$ is a function of $X$ and $S$ as well as $g$, since it depends both on what possibilities are left and on the actual secret word.

The next word picked by YAWS is given by

$$\text{argmin}_{g \in G} E[\lvert r(g, X, S) \rvert],$$

which is just the original explanation in (crappy) maths notation. We minimise (using argmin) the expected size (E[|...|]) of the new set of secret words.

The expected size can be expressed as

$$E[\lvert r(g,X,S) \rvert] = \sum_{x \in S} P(X=x) \,\lvert r(g,x,S) \rvert,$$

where each secret is equally probable, i.e. $P(X=x)=\frac{1}{\lvert S \rvert}$.

The final piece of the puzzle is to compute the new secret set $r(g, x, S)$. If we have a hint function $h$ that accepts a guess and a secret word, and returns a string representing the hint, such as "GYBBG" (green, yellow, black, black, green), then the new secret set is

$$r(g,x,S) = \{y \in S : h(g,x)=h(g,y)\}.$$

In other words, we only keep secret words that return the same hint as the true secret word.

This is great! We've fully specified how YAWS greedily picks the best next guess. The only problem is complexity. Let's say that the size of $G$ and the size of $S$ are both proportional to a number $n$. YAWS has to loop over all possible guesses, which is $\mathcal{O}(n)$ complexity. For each guess, it has to check all possible secrets, which is also $\mathcal{O}(n)$ complexity. And for each secret, it has to loop over all the other secrets to figure out which ones will be in the new set of secrets, which is - you guessed it - $\mathcal{O}(n)$ complexity. Overall, that makes it an $\mathcal{O}(n^3)$ algorithm, which is verrrrryyyy slow for Wordle's $n \approx 10000$.

A better approach is to group the secrets based on the hint they will return for a given guess $g$. Then we don't need to loop over the secrets a third time, because we already know which secrets give the same hint. This makes the complexity $O(n^2)$. Here's the improved algorithm in Python pseudocode.

def expected_size(g, S):
    buckets = collections.defaultdict(list)
    for x in S:
        buckets[h(g,x)].append(x)
    return sum(1/len(S) * len(buckets[h(g,x)]) for x in S)

If that handwavey explanation didn't lose you completely, here are the results! This is the number of guesses made by YAWS when it's tested on all possible secret words, with its first guess being RAISE. I've compared it to my first 28 Wordle scores.

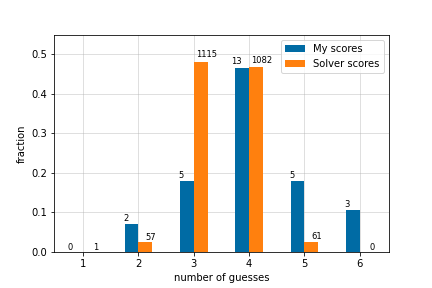
YAWS gets a score of 3 much more consistently than I do, and it never makes more than 5 guesses. It makes an average (mean) of 3.495 guesses, which is pretty close to the best possible average (3.4212). Not bad for a greedy algorithm. For a description of the optimal Wordle algorithm, I would recommend checking out this write-up, which is where I nicked some of the maths notation that I used above.

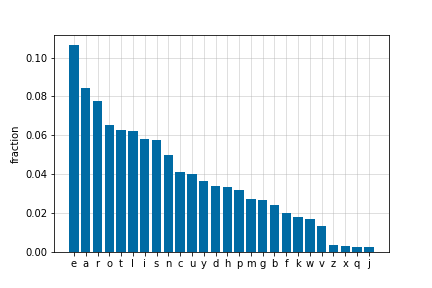
One last thing. Here's a graph of letter frequency among the Wordle secret words. ETAOIN SHRDLU is often used as a mnemonic to remember the most commonly used letters in the English language, but for Wordle it looks like that should be EAROT LISNCU.

• Back to blog
• RSS feed

I'd be happy to hear from you at galligankevinp@gmail.com.